Chapitre 10 - Primitives et Intégrales

Déterminer les primitives des fonctions usuelles par lecture inverse du tableau des dérivées
Connaître et utiliser une primitive de $x \rightarrow u'(x) e^{u (x)}$
Calculer une intégrale
Calculer l'aire du domaine délimité par les courbe représentative de deux fonctions positives

IPrimitives

1Introduction de la notion de primitive

Soit $f$ une fonction continue sur un intervalle $I$ :

$F$ une fonction dérivable sur $I$ est une primitive de $f$ si pour tout $x$ de $I$ :

$$ F'(x) = f (x)$$

Par conséquent, pour vérifier qu'une fonction $F$ est une primitive de $f$, il suffit de dériver $F$ et d'obtenir $f$.

Soient $f$ et $F$ définies par $f (x) = x$ et $F (x) = \frac{x^2}{2}$ :

On dérive $F$ : $F'(x) = \frac{2 x}{2} = x = f (x)$

Donc $F$ est bien une primitive de $f$

Dans notre cadre, on peut toujours être sûr que chercher une primitive est un problème soluble car :

Toute fonction continue $f$ admet une primitive $F$

Nous verrons dans la partie suivante, qu'en fait les primitives et les intégrales sont liées car $F (x) = \int_{0}^{x}{f (t) dt} $ définit une primitive de $f$

Une particularité des primitives par rapport aux dérivées est que si il existe toujours une primitive, il n'en existe pas forcément une seule :

Soient $f$ une fonction continue et $F$ une primitive.

Soit $G$ la fonction définie par $G (x) = F (x) + k$ (où $k$ est un nombre réel quelconque).

Alors, $G$ est aussi une primitive de $f$

Soient $f$, $F$ et $G$ :

$f (x) = x$
$F (x) =\frac{x^2}{2}$
$G (x)=\frac{x^2}{2} + 1$

Si on dérive $F$ et $G$, on retombe sur $f$, donc les deux sont des primitives de $f$

Toutes les primitives de $f$ sont similaires et diffèrent d'une constante.

En conséquence, toutes les exepressions des primitives de $f (x) = x$ sont de la forme :

$\frac{x^2}{2}$
$\frac{x^2}{2} + 1$
$\frac{x^2}{2} -1$
$\frac{x^2}{2} + 23,5$
etc.

On est donc souvent amené à chercher une primitive particulière parmi toutes :

Trouver une primitive particulière :

Soit $f (x) = x$, on cherche la primitive $F$ telle que $F (1) = 2$

On sait que la primitive recherchée est de la forme $F (x) = \frac{x^2}{2} + k$
On sait que $F (1) = 2$, donc on réécrit $\frac{1^2}{2} + k = 2$
On simplifie l'égalité obtenue : $\frac{1}{2} + k = 2$
On résoud l'équation d'inconnue $k$ : $k = 2 - \frac{1}{2} = \frac{3}{2}$
En conclusion, la primitive recherchées est $F (x) = \frac{x^2}{2} + \frac{3}{2}$

IIIntégrale d'une fonction continue sur un intervalle

1Théorème fondamental

Soit $f$ une fonction continue et positive sur $[a;b]$ et $F$ une primitive : $$\int_{a}^b{f (t) dt} = F (b) - F (a)$$

Par commodité, on note : $$F (b) - F (a) = [F (x)]_a^b$$ C'est utile quand une fonction est donnée sans nom, par son expression (voir exemples ci-dessous).

On retrouve l'aire d'un rectangle de largeur 1 et de hauteur 2 : $$\int_{0}^1{2 dt} = [2 x]_0^1 = 2\times 1 - 2\times 0 = 2$$

On retrouve l'aire d'un triangle rectangle de base 1 et de hauteur 1 : $$\int_{0}^1{x dt} = [\frac{x^2}{2}]_0^1 = \frac{1^2}{2} - \frac{0^2}{2} = \frac{1}{2}$$

Il est également possible de calculer de la même manière, l'intégrale d'une fonction continue pas forcément positive :

Soit $f$ une fonction continue sur $[a;b]$ et $F$ une primitive : $$\int_{a}^b{f (t) dt} = F (b) - F (a)$$

2Propriétés élémentaires

ALinéarité

La propriété de linéarité permet de regrouper ou un calcul de plusieurs intégrales en une seule (ou à l'inverse de séparer en plusieurs un calcul sur une seule intégrale) :

Soient $f$ et $g$ deux fonctions continues sur $[a;b]$ : $$\int_{a}^b{f (t) dt} + \int_{a}^b{g (t) dt} = \int_{a}^b{f (t) + g (t) dt}$$
Soit $\alpha$ un nombre réel : $$\alpha \int_{a}^b{f (t) dt} = \int_{a}^b{\alpha f (t) dt}$$

La linéarité permet par exemple de séparer de concentrer ses calculs d'intégrales sur les parties les plus importantes : $$ \begin{array}{ccl} & & \int_{0}^1{\frac{x}{3}x\ dx}\\ &=& \frac{1}{3}\int_{0}^1{x\ dx}\\ &=& \frac{1}{3}[\frac{x^2}{2}]_{0}^1\\ &=& \frac{1}{3}(\frac{1^2}{2} - \frac{0^2}{2})\\ &=& \frac{1}{3} \times \frac{1}{2}\\ &=& \frac{1}{6}\\ \end{array} $$

La linéarité peut s'avérer utile pour simplifier un calcul d'intégrales compliquées : $$ \begin{array}{ccl} & & \int_{0}^1{x - 1 + \sqrt{2 x + 1} dt} + \int_{0}^1{1 - \sqrt{2 x + 1} dx}\\ &=& \int_{0}^1{x - 1 + \sqrt{2 x + 1} + 1 - \sqrt{2 x + 1} dx}\\ &=& \int_{0}^1{x\ dx}\\ &=& \text{etc...}\\ \end{array} $$

BRelation de Chasles

La relation de Chasles permet aussi de simplifier des calculs d'intégrales et d'aires, mais pour une même fonction sur deux intervalles différents :

Soit $f$ une fonction continue sur $[a;b]$ et $c$ un nombre réel dans $[a;b]$ : $$\int_{a}^b{f (t) dt} = \int_{a}^c{f (t) dt} + \int_{c}^b{f (t)}$$

La relation de Chasles exprime le fait que l'aire calculée peut être séparée en deux zones comme sur la figure ci-dessous :

3Positivité

Si $f \geq 0$, alors $\int_{a}^b{f (t) dt} \geq 0$
Si $f \leq 0$, alors $\int_{a}^b{f (t) dt} \leq 0$

Si il faut trouver l'aire au dessus d'une courbe négative le calcul de l'intégrale donnera un résultat négatif (par exemple $-3$). Il faudra donc répondre à la question posée en prenant la valeur absolue du résultat (par exemple $3$).

Lorsqu'une courbe n'est ni positive ni négative (comme ci-dessous), le calcul de l'aire représentée se fait en séparant les zones :

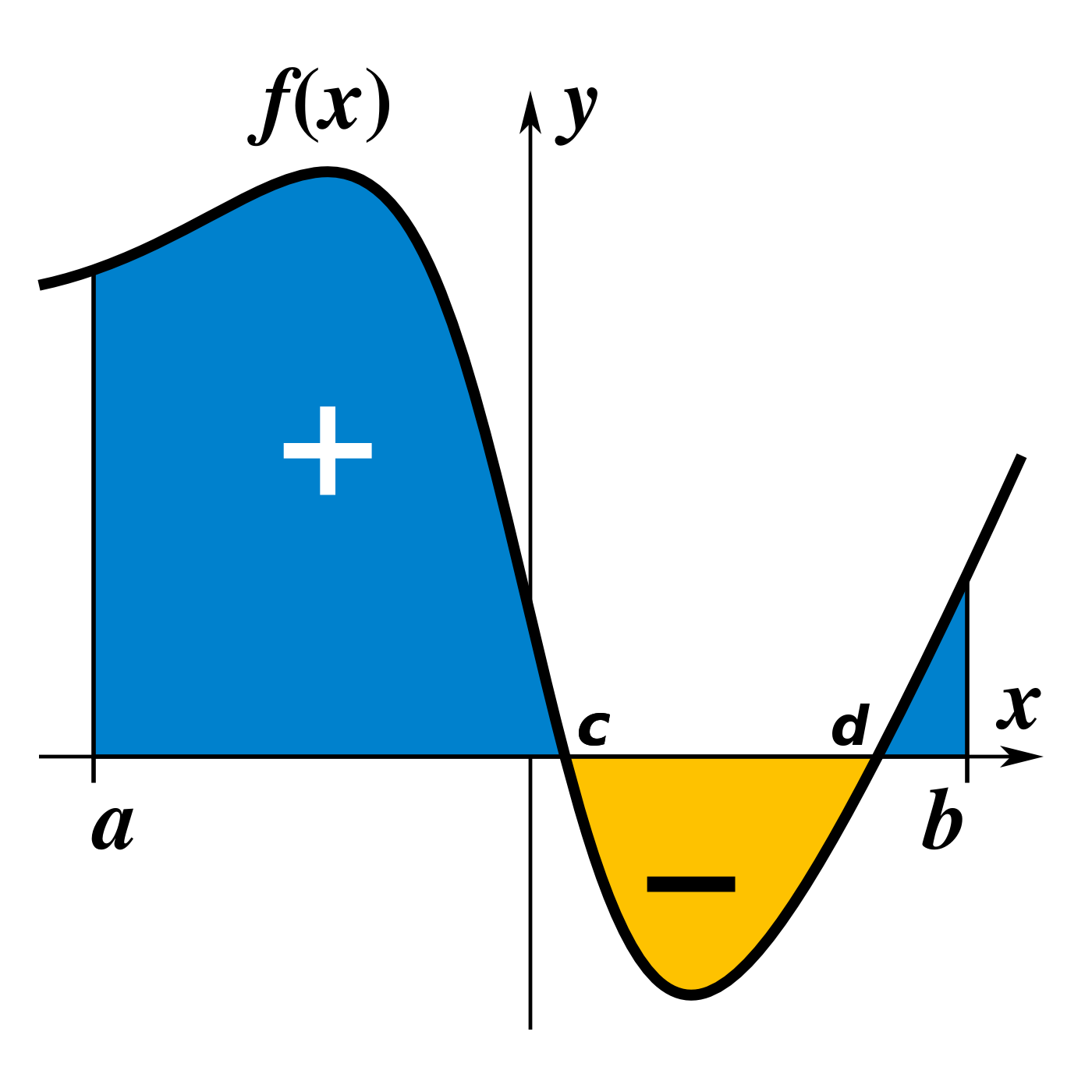
On calcule la première aire bleue $\int_a^c{f (x) dx}$
On calcule la valeur absolue de l'aire jaune $|\int_c^d{f (x) dx}|$
On calcule la deuxième aire bleue $\int_d^b{f (x) dx} + \int_c^b{f (x) dx}$

Le résultat sera la somme des trois aires.

Si on calcule directement $\int_a^b{f (x) dx}$, on trouvera un résultat plus petit car l'intégrale négative aura "compensé" une partie de l'intégrale positive.

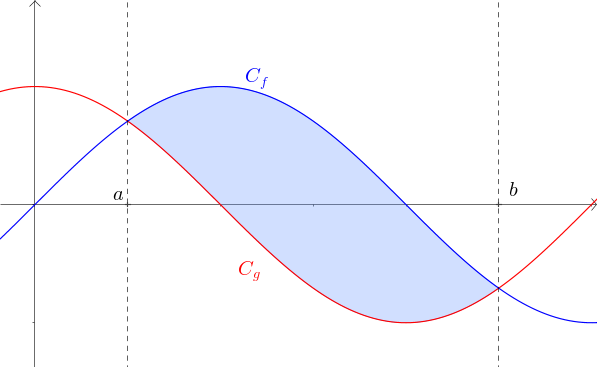
4Aire entre deux courbes

Soient $f$ et $g$ deux fonctions continues sur $[a;b]$, de courbes représentatives $C_f$ (au dessus) et $C_g$ (en dessous).

L'aire comprise entre $C_f$ et $C_g$ sur l'intervalle $[a;b]$ vaut :

$$\int_{a}^b{f (t) - g (t) dt}$$

5Valeur moyenne

Soit $f$ une fonction continue sur $[a;b]$.

La valeur moyenne prise par la fonction $f$ sur $[a;b]$ vaut :

$$\frac{1}{b - a}\int_{a}^b{f (t)dt}$$

L'aire sous la courbe est égale à l'aire sous le rectangle de hauteur la valeur moyenne :